Vystudovala jsem matematiku a historii se zaměřením na vzdělávání, a proto jsem se rozhodla dovednosti získané při studiu těchto oborů využít v mé bakalářské i diplomové práci. V článku čtenáře v krátkosti seznámím s vybranými učebnicemi matematiky ze 17.‒19. století, ze kterých jsem čerpala, a představím postup vytváření úloh. Do článku jsem dále vybrala několik úloh, které zastupují všechny roviny inspirace získané při studiu pramenů. U příkladu o výměře pozemku jsem se inspirovala přímo textem a myšlenkami pramene. Zadání jsem poupravila do současné podoby, ale obdobný příklad se nachází i ve výchozím spisu. Druhou rovinou inspirace je řešení, které autor nabízel. Toto řešení čtenář nalezne i v tomto článku. Inspirativní byly rovněž obrázky znázorňující zadání úloh. Jako příklad uvádím úlohu o zjišťování výšky hradeb. A poslední rovinou inspirace jsou definice matematických pojmů a věty, které jsem přepsala a připojila ke každému příkladu. Do tohoto článku jsem vybrala Pythagorovu větu ze Sedláčkovy publikace. Svým zaměřením úlohy spadají do tematických oblastí planimetrie, funkčních vztahů a trigonometrie. Svou náročností pak úlohy pokrývají učivo základní (RVP ZV 2021) i střední školy (RVP G 2007). K úlohám jsou připojeny ilustrace a odkazy na aplety ve formě webového odkazu a QR kódu.
Problematika řešení slovních úloh
Slovní úlohy jsou nedílnou součástí hodin matematiky. Skrze ně mohou být naplňovány některé cíle Rámcového vzdělávacího programu vzdělávací oblasti Matematika a její aplikace (např. schopnost matematizovat reálnou situaci, používání matematiky v reálných situacích). Zároveň jsou jednou z problematických oblastí na 1. I 2. stupni, a proto je vhodné jim věnovat pozornost. Žáci se při řešení mohou uchylovat k povrchovým strategiím, které umožňují vytvořit řešení bez situačního modelu (představy situace). Takové řešení nerozvíjí žákovu schopnost matematizovat situace a u složitějších úloh pak může žák selhat. Mezi příčiny takového jednání se řadí snaha najít úlohu podobnou, u které má žák již vytvořené schéma řešení. Toto řešení pouze „překopíruje“, avšak bez bližšího porozumění úloze (Vondrová, 2020). Proto je dobré hledat nevšední zadání úloh. Zdrojem takových zadání mohou být historické prameny.
Historické prameny jako zdroj inspirace
Historický pramen ve svém širším pojetí zahrnuje veškerý materiál, který může historie využít jako zdroj poznání (Dvořák a Borovský, 2014, s. 47). Jako prameny můžeme označit i matematické spisy a učebnice, které tu zanechali naši předchozí kolegové. Čím hlouběji postupujeme do minulosti, tím více se zadání matematických úloh odlišují od těch současných, proto jsem vybrala prameny, které vznikly v 17.–19. století.
První z využitých pramenů je Knížka o měrách zemských a vysvětlení od kterého času míry a měření zemské v Království českém svůj začátek mají, jejímž autorem je zeměměřič Šimon Podolský z Podolí.[1] Příručka byla vydána v první polovině 17. století a věnuje se vývoji a proměnám měrných jednotek v Království českém. Podolský upozorňuje na nejednotnost měr a jejich škodné užívání.
Druhým pramenem je dílo Gruntovní počátek matematického umění Václava Josefa Veselého z Veselí[2] vydané v 18. století. Oproti předchozí příručce je značně obsáhlejší a propracovanější. Dílo je rozděleno na část teoretickou a část praktickou. V teoretické části autor uvádí stručné definice matematických pojmů a vztahů. Praktická část je věnována aplikačním úlohám a situacím, se kterými se mohl měřič setkat. Jedná se například o zjišťování hloubky dolu.
Posledním pramenem, který jsem využila, je spis vydaný roku 1822 Josefem Vojtěchem Sedláčkem.[3] Kniha Základové měřictví čili Geometrie je obsáhlou publikací, která se skládá z pěti částí, které jsou logicky řazeny a postupně prohlubují poznatky o praktickém využití geometrie. Publikace obsahuje řadu pojmů, u kterých jsou uvedeny jejich další česká synonyma a také latinské i německé názvy. Definice a věty jsou doplněny důkazy a řadou příkladů, na nichž je učivo aplikováno. U příkladů je uvedeno jejich řešení, které autor zpracoval velmi podrobně a snaží se jej jednoduše vysvětlit. Nechybí ani odkazy na obrázky znázorňující zadání úloh. Obrázky se nachází na konci knihy za seznamem nejdůležitějších pojmů (např. přímka, čtverec, trojúhelník).
Vytváření úloh
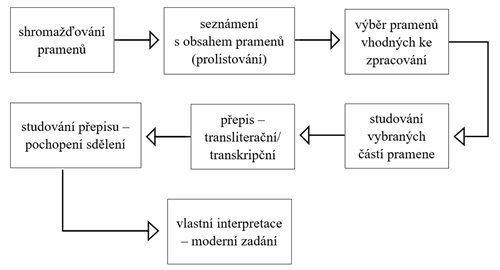
Práce s historickými učebnicemi a příručkami je velmi náročná a vyžaduje spoustu času. Při zpracovávání úloh se mi osvědčil postup, který jsem znázornila do schématu (viz obr. 1 - v galerii). Pokud by se čtenář chtěl více seznámit s jednotlivými kroky, nalezne je okomentované v mé práci.
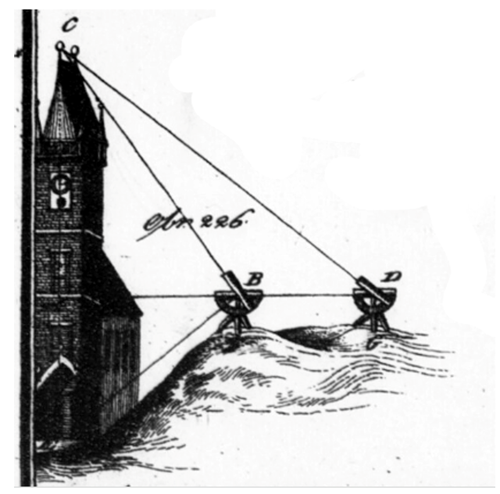
Pro ty, kteří by si chtěli tuto práci vyzkoušet, jsem vybrala úryvek z učebnice Václava Josefa Veselého z Veselí (viz obr. 2 - v galerii). Jedná se o popis postupu zjištění výšky objektu, pokud nemáme k dispozici měrné instrumenty. Pod ukázkou textu naleznete transkripční přepis (přepis textu s ohledem na současná pravidla pravopisu), který poslouží jako kontrolní text. A v neposlední řadě je uveden příklad zadání úlohy současným způsobem.
Úryvky z pramenů lze využít i v hodinách matematiky (případně dějepisu). U originálního textu by žáci dostali za úkol odhalit grafická pravidla pro psaní písmen. Dalším úkolem by bylo text nebo jeho část přepsat. Žákům můžeme nabídnout i ukázku přepsanou (vhodné jsou matematické definice a věty, které se v práci nacházejí v historickém okénku) a úkolem žáků by bylo odhalit, o jaký pojem nebo větu se jedná.
Další nedílnou součástí práce s pramenem je jeho rozbor. Sem spadají otázky: Kdo je autorem pramene? Kdy pramen vznikl? Co je obsahem pramene? Komu je pramen určen? Jaký je záměr pramene? Tento analytický přístup vyžaduje nejdříve nácvik na jednoduchých textech. Práce s historickými prameny rozvíjí u žáků kritické a historické myšlení (Labischová, 2010, s. 47).
Transkripční přepis
To se také může bez instrumentu udělat, a to jest ten nejsprostější naturální způsob. Kdež to sedlákům jako jejich inventi, aneb při nejmenším jejich praxi přivlastněno jest. Totiž, když vezme jednu tyčku, něco delší nežli sám jest, a strčí ji zrovna do země. A to, aby tak dlouze od země vycházela, jako ten člověk jest. A položí se za ni v jednu linii s tou tyčkou a se stromem a to tak, aby nohy na té tyčce stát přišly. A hledí se přes ten hořejší konec tyčky. Když ale v takový linii špici toho stromu, aneb věci, které výšku žádá vědět, ještě nevidí, tak postrčí takovým způsobem s tyčkou a sám sebou tak dlouho před sebe, aneb za sebou, až tím způsobem špici toho stromu vidí. A když najde, tak měří od toho místa, kde jeho hlava ležela, v jedné linii až k tomu stromu kroky [?][4]. A jest ujištěný, že ten strom rovně tak dlouhý jest jako délka od toho místa, kde jeho hlava ležela až k tomu stromu. Ta věc jest lehká k vyrozumění a sedlák má dobře, kteréž z následujícího více viděti bude.
Zadání
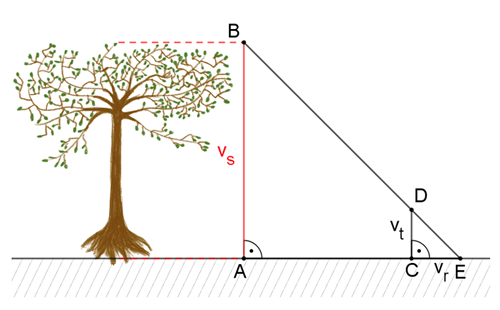
Rolník chce zjistit výšku stromu, který stojí na jeho pozemku. K dispozici má pouze tyčku, která je přibližně stejně vysoká jako on. Najde si vhodné místo a tyčku umístí do země tak, že z polohy vleže vidí současně špičku tyčky a stromu a jeho nohy se dotýkají tyčky. Jaká je výška stromu, jestliže rolník měří 187 cm a vzdálenost naměřená mezi stromem a tyčkou je 7 metrů? (viz obr. 3 - v galerii).
(úloha pro ZŠ)
Vybrané úlohy
Na základě studia historických příruček lze postup měřiče rozdělit do dvou etap. První etapou je vlastní měření potřebných délek a úhlů nezbytných pro výpočet požadovaného prvku. Do druhé etapy spadá aplikace matematických znalostí a následný výpočet. V historických příručkách, které jsem procházela, jsou situace zobecněny a u každého typu úlohy je uvedeno řešení. V řešení jsou podrobně popsány kroky vlastního měření v terénu a poté autor uvádí matematické (zpravidla numerické) řešení. Tuto strukturu jsem zachovala, kroky popsala v zadání a přidala naměřené hodnoty. Při čtení zadání žáci s měřičem postupně procházejí všemi kroky první etapy. Řešení úloh představuje etapu druhou.
Jednou z příčin neúspěšnosti řešení úloh je neschopnost vytvořit matematický model situace. U geometrických úloh je model situace zvlášť důležitý, neboť napomáhá rozklíčovat vztahy mezi objekty a nalézt vhodné řešení. Zadání obsahující jednotlivé kroky společně s reálnou situací by mohlo podpořit žákovu představu a pomoct s tvorbou modelu situace (Vondrová, 2020).
Výměra pozemku (úloha pro ZŠ)
Zadání
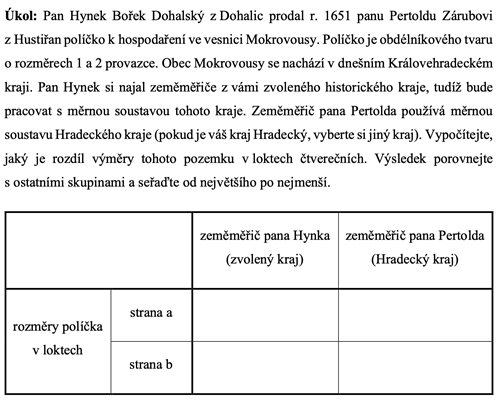
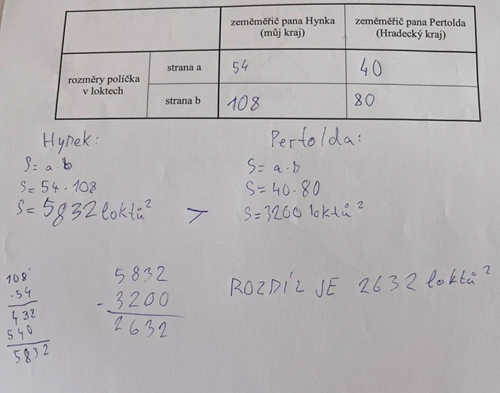
Pan Hynek Bořek Dohalský z Dohalic prodal r. 1651 panu Pertoldu Zárubovi z Hustiřan políčko k hospodaření ve vesnici Mokrovousy. Políčko je obdélníkovitého tvaru o rozměrech 1 a 2 provazce. Zeměměřič pana Hynka použil měrnou soustavu, kde je jeden provazec dlouhý 42 loktů[5]. Avšak v kraji pana Pertolda se používá novější soustava, kde je jeden provazec dlouhý 52 loktů. Vypočítejte, jaký je rozdíl výměry tohoto pozemku. Kdo by se ošidil, kdyby se cena pozemku vypočítala podle soustavy pana Hynka?
https://www.geogebra.org/m/nz2naemk
Řešení
Nyní si představíme řešení, které nám nabídnul Podolský ve své příručce. Políčko má tvar obdélníku a délky jeho stran označíme a a b. Pro měrnou soustavu pana Hynka použijeme označení aH a bH a pro soustavu pana Pertolda aP a bP. Strana a je rovna délce jednoho provazce a strana b délce dvou provazců. Nyní si každou délku strany převedeme na lokty:
aH = 1 provazec = 42 loktů aP = 1 provazec = 52 loktů
bH = 2 provazce = 84 loktů bP= 2 provazce = 104 loktů.
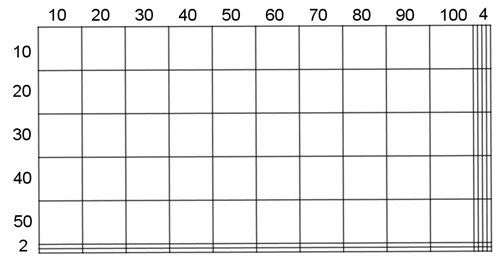
Políčko si zakreslíme do čtvercové sítě s délkou 10 loktů na jednu stranu čtverce. Lokty, které nám budou přebývat, zakreslíme jako obdélníčky (viz obr. 4 - v galerii).
Nejprve si nakreslíme políčko pro měrnou soustavu pana Pertolda, které je vybarveno šedě a pokrývá celou čtvercovou síť. Poté do téže sítě umístíme políčko vyměřené měřičem pana Hynka tak, že ho ukotvíme v pravém dolním rohu. Toto políčko je vyšrafováno (viz obr. 5 - v galerii).
Čtverce a obdélníčky, které zůstaly šedé, dávají dohromady rozdíl výměry pozemku. Početně to provedeme tak, že sečteme obsahy všech těchto čtverců a obdélníčků, což je 1880 loktů čtverečních. Z obrázku je patrné, že políčko vyměřené měřičem pana Pertolda je větší, tudíž i jeho cena bude vyšší. Cena políčka je stanovena na základě soustavy pana Hynka, tudíž cena bude nižší, než kterou by zaplatil pan Pertold, pokud by užil měrné soustavy svého zeměměřiče. Z toho usuzujeme, že se ošidil pan Hynek.
Další řešení ponechám na čtenáři a jeho znalostech matematiky základní školy.
Výška hradeb (úloha pro SŠ)
Zadání
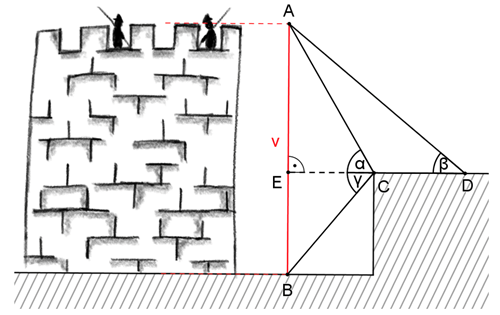
Úkolem měřiče je zjistit výšku hradeb, které jsou lemovány hradním příkopem. Hradby bude měřit zvenčí. Představí si horizontální linii vedoucí od okraje příkopu k hradbám a změří si úhly, které tato linie svírá s horním okrajem hradeb a dnem příkopu. První z úhlů je roven 60° a druhý 50°. Dále si od tohoto okraje změří úsek, který je dlouhý 5 metrů a směřuje od hradeb. Z druhého konce úseku si opět změří úhel s horním okrajem hradeb, který činí 40°.
https://www.geogebra.org/m/zyfphwva
Historické okénko
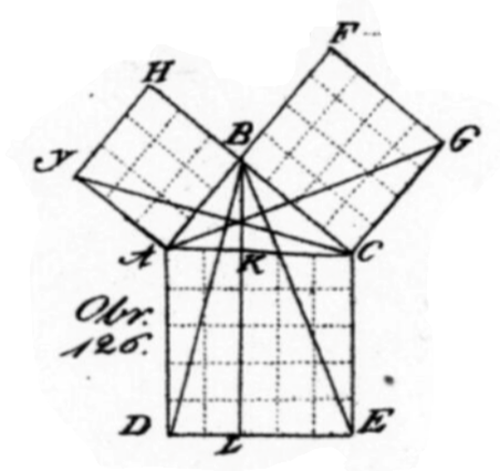
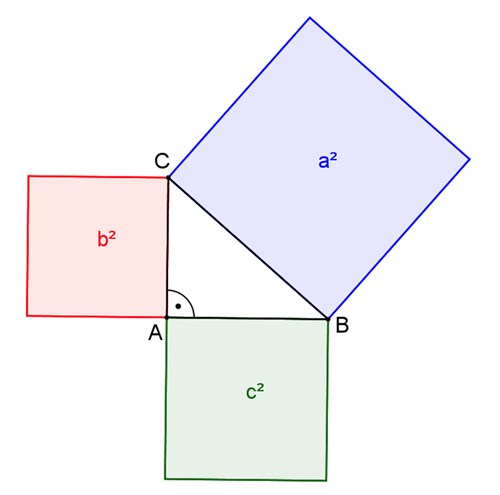
„V každém přímoúhelném trojúhelníku, kdybychom jak na přeponě, tak na odvěsnách sestrojili čtverce. Ploskost čtverce na přeponě vystaveného sama pro sebe obsahuje již zaúplna tolik jako ploskosti čtverců na obou odvěsnách vystavených součtem vzaté. To jest čtverec přepony jest stejný s čtverci obou odvěsen součtem vzatými.
Poučku tu nazýváme Pythagorickou, poněvadž ji onen veliký filosof Pythagoras téměř 500 let před narozením Krista pána nalezl“ (Sedláček, 1822, s. 90–91).
Z praxe
Ve své diplomové práci jsem navázala na bakalářskou práci a vytvořila úlohy podobným způsobem, jak bylo popsáno v tomto článku. Jelikož jsem neměla sama možnost úlohy vyzkoušet ve třídě, poprosila jsem o pomoc učitele. Úlohu jsem upravila pro skupinovou práci, při které žáci vyhledávali data v tabulce a zjišťovali rozdíl výměry pozemku (viz obr. 10 a 11 - v galerii) Paní učitelka měla před ověřováním úlohy obavu, že úloha žáky nebude bavit. Byla mile překvapena, že se setkala s pozitivním ohlasem u žáků.
Závěrem
Problematika slovních úloh zahrnuje mnoho proměnných, které mohou ovlivnit úspěšnost jejich řešení. Žáci se uchylují k hledání podobných úloh, u kterých již řešení znají, a to pak aplikují na další úlohu, aniž by vytvořili situační model úlohy. Abychom žáky přivedli k tvorbě situačního modelu, je vhodné hledat nevšední zadání úloh. Takové zadání jsem vytvořila na základě studia matematických pramenů. Úlohy představují praktické využití geometrických poznatků při práci měřiče. Znázorňují reálné situace a problémy, které by mohly pomoci při tvorbě situačního modelu a následného řešení úlohy (Vondrová, 2020, s. 84). Úlohy se rovněž podílejí na utváření historické představy o tehdejší společnosti. Seznamují žáky s českými jednotkami délky, které jsou součástí českých dějin a kultury. Nevšední úlohy a aktivity plní rovněž motivační funkci a mohou zvýšit zájem o předmět. Motivující je pro žáky také práce s prameny (Labischová, 2008, s. 47). Historické texty a úlohy se nabízejí k využití ve výuce nebo v projektovém vyučování zaměřeném na mezipředmětové vztahy matematiky a historie. Doufám, že článek bude pro někoho z čtenářů inspirací k novým námětům do hodin matematiky, které budou mít nádech historie našich krajin.
Mgr. Michaela Němečková
Je absolventkou magisterského oboru Učitelství matematiky a dějepisu pro 2. stupeň ZŠ na Jihočeské univerzitě v Českých Budějovicích. Na této univerzitě již vystudovala obor matematika a historie se zaměřením na vzdělávání. V roce 2020 vyhrála se svou bakalářskou prací SVOČ v didaktice matematiky. V současnosti vyučuje na 2. základní škole v Chebu.
Zdroje
Dvořák, T., & Borovský T. (2014). Úvod do studia dějepisu. Brno: Masarykova univerzita. ISBN 978-80-210-7016-5.
Labischová, D., & Gracová, B. (2008). Příručka ke studiu didaktiky dějepisu. Ostrava: Ostravská univerzita.
Mikulčák, J., & Bečvář, J. (2010), ed. Nástin dějin vzdělávání v matematice (a také školy) v českých zemích do roku 1918. Praha: Matfyzpress. Dějiny matematiky. ISBN 978-80-7378-112-5.
Němečková, M. (2020). Sbírka úloh z matematiky inspirovaná historickými prameny (Bakalářská práce). České Budějovice: Jihočeská univerzita v Českých Budějovicích.
Petty, G. (2013). Moderní vyučování. Praha: Portál.
Podolský z Podolí, Š. (1683).Knižka o Měrách Zemských: a wyswětlenj, Od kterého CžasuMjry, a Měřenj Zemské, W KrálowstwjCžeskémswůg začátek magj. Wytisstěná w Praze. Dostupné také z:
http://www.manuscriptorium.com/apps/index.php?direct=record&pid=NKCR__-NKCR__54_E_002132_0H8KDQF-cs#search.
Rámcový vzdělávací program pro gymnázia. (2007). Praha: Výzkumný ústav pedagogický v Praze. Dostupné z: http://www.nuv.cz/file/159.
Rámcový vzdělávací program pro základní vzdělávání. (2021). Praha: MŠMT. Dostupné z: https://www.msmt.cz/file/56005/.
Sedláček, J. V. (1822).Základowéměřictwj, čili, Geometrye. W Praze: u wdowy Jozefy Fetterlowé z Wildenbrunu w knjžecýarcybiskupské knihtiskárně w Semináryum. Dostupné také z: https://kramerius5.nkp.cz/uuid/uuid:0c25f160-bdd1-11dc-964a-000d606f5dc6.
Veselý, V. J. (1734). Gruntownj Počátek MathematickéhoVměnjGeometriaPractica, Trigonometria Plana Stereometria. VžjwánjTabellarum, Sinuum, a Logarithmorum. Wytisstěno w Praze. Dostupné také z: http://www.manuscriptorium.com/apps/index.php?direct=record&pid=NKCR__-NKCR__54_D_000147_15930R2-cs#search.
Vondrová, N. (2020). Příčiny používání povrchových strategií řešení slovních úloh a jak jim předcházet. Učitel matematiky, 28(2), 66-93.
Odkazy v textu
[1] Šimon Podolský z Podolí (1562–1617) byl zeměměřič, který zároveň i zhotovoval mapy šlechtických panství. Působil i na panství Petra Voka z Rožmberka (Mikulčák, 2010, s. 74–75).
[2] Václav Josef Veselý z Veselí (1683–1736) byl přísežným zemským mlynářem a geometrem (Mikulčák, 2010, s. 69).
[3] Josef Vojtěch Sedláček (1785–1836) byl kněz řádu premonstrátů a profesor matematiky na gymnáziu v Plzni. Společně se Stanislavem Vydrou se zasloužil o položení základů české matematické terminologie (Mikulčák, 2010, s. 125).
[4] V hranatých závorkách se uvádí ty části textu, které nebyly čitelné.
[5] český loket = 59,27 cm
český provazec = 30,82 m