Učit STEM integrovaně, nebo v mezipředmětových vztazích?

duben 2023 Helena Koldová, Lukáš Rokos

Pedagogická fakulta Jihočeské univerzity v Českých Budějovicích si vytvořila vizi přípravy studentů učitelství, kterou označila názvem „Učitel Pro Futuro“ – učitel pro budoucnost. Abychom dostáli tomuto konceptu, inovujeme svou výuku a seznamujeme studenty s novými přístupy ve výuce přírodovědných předmětů, například s integrovanou výukou. Přemýšleli jsme, jak si poradíme s výukou přístupu integrované výuky ve dvou našich kurzech, didaktiky matematiky a didaktiky přírodopisu. Přinášíme pohled na tři ilustrativní úlohy, s jejichž pomocí se zamýšlíme nad výhodami a nevýhodami uvedeného přístupu a ukazujeme naše zkušenosti v přípravě budoucích učitelů.

Integrovaná výuka – proč se o ní hovoří?

Charakteristickým rysem dnešní doby je globalizovaný pohled, tj. vnímání a poznávání okolního světa v souvislostech. V moderní edukaci evidujeme taktéž požadavky na výuku v souvislostech, například ve formě integrace vyučovacích předmětů i vzdělávacích obsahů, a to nejen ve světě, ale i v České republice (Koldová et al., 2020; Skalková, 2006). S nástupem Rámcově vzdělávacího programu pro základní vzdělávání (RVP ZV^[1]) v roce 2005 jsme se poprvé potkali se spojením vzdělávacích obsahů do nových vzdělávacích oblastí: Člověk a jeho svět, Člověk a svět práce, Člověk a příroda. V současné době diskutujeme o nových přístupech ke vzdělávání, jako je metoda CLIL (z angl. Content Language Integrated Learning), STEM (z angl. Science, Technology, Engineering and Mathematics) apod. Abychom se mohli těmto konkrétním přístupům detailněji věnovat a rozhodnout se, zda je budeme chtít použít ve vlastní výuce, tak si nejprve stručně vysvětleme některé základní pojmy, které s nimi souvisejí.

Integrovaná výuka – co znamená?

Integrovaná výuka umožňuje uplatnění různých (mezipředmětových, logických, strukturních, analogických) vazeb v obsahu jednotlivých vzdělávacích oblastí a zejména pak propojení teoretických poznatků s praktickými činnostmi žáků. Realizování integrované výuky v současné škole lze opírat o integrovaná témata zařazená do tradičních učebních předmětů, která však mohou být později základem pro integrované formy výuky a obsahovým jádrem pro nově vytvářené integrované předměty, v nichž již bude komplexněji využíváno propojení obsahů několika vědních oblastí (Podroužek, 2002). Model plně integrované výuky by měl bourat umělé zdi mezi jednotlivými kurikulárními oblastmi (Kovaliková & Olsenová, 1995). Pracujme s vymezením, v němž integrovanou výuku chápeme jako výuku sjednocující více vzdělávacích obsahů do jednoho integrovaného předmětu, s cílem realizace mezipředmětových vztahů (Koldová et al., 2020).

Mezipředmětové vztahy a jejich vztah k integrované výuce

Mezioborovost, víceoborovost napříč vědními obory či průřezovost je přístup, který zkoumá problém, klíčový obvykle pro jednu disciplínu, prostřednictvím pohledu jiné disciplíny. Z toho pak můžeme usoudit, že učení v mezipředmětových vztazích se týká vzdělávacích aktivit, které souvisejí s předmětem mimo rozsah dané disciplíny bez jakékoli integrace z jiných disciplín (Průcha, Walterová & Mareš, 2003). Pokud chce učitel používat interdisciplinární přístup, tak například zadává speciální úlohy, v nichž žáci musí použít poznatky z různých předmětů, aby došlo k řešení komplexního problému (Průcha et al., 2003).

Podle Janáse (1985) se termínem mezipředmětové vztahy obvykle označuje široká oblast didaktických vazeb, které se týkají nejen obsahu vyučování. Příkladem mohou být obsahové vazby (odraz mezivědních vztahů a reflektování obsahové shody učiva), metodické vazby (použití společných metod a forem vyučování a učení) a časové vazby (návaznost učiva v čase).

Rámcové vzdělávací programy při vytváření školních vzdělávacích programů (ŠVP) doporučují školám zařadit mezipředmětové souvislosti (další synonymum k termínu mezipředmětové vazby), případně další poznámky upřesňující realizaci vzdělávacího obsahu.

Výhody, nevýhody a rozdíly

Integrovaná výuka i výuka v mezipředmětových vztazích může být jedním z nástrojů k rozvíjení klíčových kompetencí žáka. Často se úlohy, zadávané v obou přístupech, týkají situací z reálného života a motivují žáky k řešení úloh a problémů (Dareová, Ellis & Roehrigová, 2018), učí je vyhledávat a zjišťovat potřebné informace k řešení problému, pracovat s literaturou, třídit získané poznatky a přemýšlet v souvislostech (Berlandová & Steingutová, 2016). Nedílnou součástí integrované výuky je rozvoj schopnosti spolupráce mezi žáky, popř. skupinami žáků. Integrované úlohy přispívají ke kultivaci žákovských postojů, utvářejí u žáků vhodné zájmy a napomáhají rozvíjet také morální a volní vlastnosti, například systematičnost, cílevědomost, svědomitost nebo soustředění na práci.

Je ovšem samozřejmé, že jakákoli metoda výuky, hodnocení nebo uspořádání obsahu s sebou nese určitá rizika. Mezi rizika zařazení integrované výuky patří především malé množství již zpracovaných a ověřených aktivit, učebních textů v českém jazyce, které by byly učitelům k dispozici. Jejich příprava je náročná a vyžaduje vyhledávání více zdrojů z určité oblasti zájmu. Proto aby integrované úlohy obsahovaly všechny potřebné požadavky, je vhodné připravovat je společně s dalšími učiteli (Rakoušová, 2008). Určitým limitem je i nedostatek zkušeností učitelů, jelikož stále není k dispozici dostatečná metodická a didaktická podpora, propracovaný systém mentoringu a možnost (virtuálních) hospitací.

Příklady ilustrativních úloh

V následujícím textu představíme aktivity, které považujeme za příklad úloh vhodných pro integrovanou výuku či výuku v mezipředmětových vztazích. Na závěr shrneme základní vlastnosti všech tří výukových aktivit a ukážeme si rozdíly mezi nimi. Otevřeme diskuzi o jejich využití ve výuce a naplnění jejich cílů.

Úloha 1 – mezipředmětová

Jako příklad interdisciplinárního přístupu můžeme uvést úlohu 1 (obr. 1 - v galerii) z učebnice Geometrie 7 nakladatelství Fraus (Binterová, Fuchs & Tlustý, 2008). Vzdělávací obsah uvedené úlohy 1 je interdisciplinárně (mezipředmětově) transformován ze vzdělávacích oblastí Matematika a její aplikace a Člověk a příroda.

V souvislosti s RVP ZV je možné vysledovat, že tato úloha klade důraz na uvědomění si užitečnosti přírodovědných poznatků a možností jejich aplikace v každodenním životě, ale také na pochopení významu užití různých technologií.

V úloze 1 jsou proto naplňovány očekávané výstupy ve vzdělávacích oblasti Člověk a příroda, konkrétně v oborech Fyzika (F), Přírodopis (P) a vzdělávací oblasti Matematika a její aplikace (M), v okruhu Závislosti, vztahy a práce s daty:

• F-9-3-01p: (žák) využívá poznatky o zákonitostech tlaku v klidných tekutinách pro řešení jednoduchých praktických problémů,
• P-9-5-01: (žák) určí polohu a objasní stavbu a funkci orgánů a orgánových soustav lidského těla, vysvětlí jejich vztahy,
• M-9-2-04: (žák) vyjádří funkční vztah tabulkou, rovnicí, grafem,
• M-9-2-05: (žák) matematizuje jednoduché reálné situace s využitím funkčních vztahů (MŠMT, 2021, s. 35, 65, 73).

Prohlédněme si podrobně úlohu 1, promysleme její zacílení a adekvátnost cílů v souvislosti s ambicemi naplnění uvedených očekávaných výstupů vzdělávacích oblastí.

Úloha 2 – aplikační

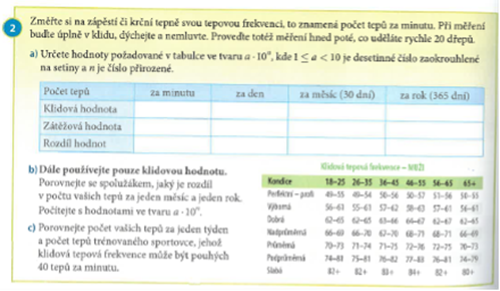
Druhá úloha (obr. 2 - v galerii), která je zadána mezipředmětově, je převzata z učebnice Matematika 8 nakladatelství Didaktis (Brlicová et al., 2022).

Tuto úlohu zde uvádíme z toho důvodu, abychom se čtenáři diskutovali rozdíl mezi úlohou 1 a úlohou 2. Pokud si pozorně promyslíme cíle, které by úloha 2 měla naplnit, očekávané výstupy a její mezipředmětovost, dojdeme k závěru, že úloha 2 transformuje vzdělávací obsah ze stejných vzdělávacích oblastí jako předchozí úloha a zaznamenáváme i přesah do vzdělávací oblasti Člověk a zdraví. Mezipředmětově úloha propojuje obory Matematika (M), Přírodopis (P) a Tělesná výchova (TV). Úloha naplňuje následující očekávané výstupy:

• M-9-2-01: (žák) vyhledává, vyhodnocuje a zpracovává data,
• M-9-2-02: (žák) porovnává soubory dat,
• M-9-2-04: (žák) vyjádří funkční vztah tabulkou, rovnicí, grafem,
• M-9-2-05: (žák) matematizuje jednoduché reálné situace s využitím funkčních vztahů,
• P-9-5-01: (žák) určí polohu a objasní stavbu a funkci orgánů a orgánových soustav lidského těla, vysvětlí jejich vztahy,
• TV-9-3-07 (žák) zpracuje naměřená data a informace o pohybových aktivitách a podílí se na jejich prezentaci (MŠMT, 2021, s. 35, 73, 98).

Na první pohled by se podle výčtu zasahujících očekávaných výstupů mohlo zdát, že je druhá uvedená úloha komplexnější a že je mezipředmětové zaměření úlohy větší. Po důkladném rozboru otázek v úloze 2 je však zřejmé, že autoři cílí především na naplnění očekávaných výstupů z oboru Matematika a její aplikace. Další očekávané výstupy z oborů Přírodopis a Tělesná výchova jsou v úloze 2 pouze implicitně skryty, otázky k jejich naplnění necílí, zatímco v úloze 1 jsou otázky pokládány napříč mezi předměty. Mohli bychom ji proto označit jako úlohu aplikační.

Prohlédněme si podrobně i tuto úlohu 2, promysleme její zacílení a adekvátnost cílů, v souvislosti s ambicemi naplnění uvedených očekávaných výstupů vzdělávacích oblastí a sledujme rozdíly mezi oběma úlohami 1 a 2.

Úloha 3 – integrovaná

Třetí úloha (obr. 3 - v galerii) je koncipována jako aktivita založená na integraci vzdělávacích obsahů. Vytvořili jsme ji pro kurz integrovaných didaktik matematiky a přírodopisu, pro studenty studijních programů učitelství pro druhý stupeň základní školy. Úloha je modifikována z originálu Elevation 5280 Cellular Respiration Task využívaného na University of Colorado, Boulder (s laskavým svolením autorky prof. Erin Furtak). Na obrázku 3 je z důvodu rozsáhlosti úlohy uvedena jen její část a celé zadání čtenář nalezne na následujícím odkazu: http://www.hyperspace.cz/ulohy/inegrovanyvzdobsah148652webcast.html.

Zadání této úlohy nyní rozebereme z toho důvodu, abychom se čtenáři diskutovali rozdíl mezi úlohou 1, 2 a 3. Pokud si pozorně promyslíme záměr autorů, cíle, které by úloha 3 měla naplnit, očekávané výstupy a její mezipředmětovost, dojdeme k závěru, že úloha 3 transformuje vzdělávací obsah ze stejných vzdělávacích oblastí jako předchozí úloha 2, navíc je směřována k naplnění očekávaných výstupů vzdělávací oblasti Cizí jazyk (DCJ) a vzdělávací obsah vzdělávacího oboru Zeměpis (Z) a Výchova ke zdraví (VZ).

Úloha naplňuje následující očekávané výstupy:

• M-9-2-01: (žák) vyhledává, vyhodnocuje a zpracovává data,
• M-9-2-02: (žák) porovnává soubory dat,
• M-9-2-04: (žák) vyjádří funkční vztah tabulkou, rovnicí, grafem,
• P-9-1-01: (žák) rozliší základní projevy a podmínky života, orientuje se v daném přehledu vývoje organismů,
• P-9-5-01: (žák) určí polohu a objasní stavbu a funkci orgánů a orgánových soustav lidského těla, vysvětlí jejich vztahy,
• P-9-5-04: (žák) rozlišuje příčiny, případně příznaky běžných nemocí a uplatňuje zásady jejich prevence a léčby,
• Z-9-2-03: (žák) porovná působení vnitřních a vnějších procesů v přírodní sféře a jejich vliv na přírodu a na lidskou společnost,
• Z-9-3-02: (žák) porovnává a přiměřeně hodnotí polohu, rozlohu, přírodní, kulturní, společenské, politické a hospodářské poměry, zvláštnosti a podobnosti, potenciál a bariéry jednotlivých světadílů, oceánů, vybraných makroregionů světa a vybraných (modelových) států,
• DCJ-9-1-03: (žák) rozumí základním informacím v krátkých poslechových textech týkajících se každodenních témat,
• VZ-9-1-03: (žák) vysvětlí na příkladech přímé souvislosti mezi tělesným, duševním a sociálním zdravím; vysvětlí vztah mezi uspokojováním základních lidských potřeb a hodnotou zdraví,
• TV-9-3-07 zpracuje naměřená data a informace o pohybových aktivitách a podílí se na jejich prezentaci (MŠMT, 2021, s. 28, 35, 71, 73, 76, 91, 97, 98).

Jak již bylo zmíněno, úloha je komplexnější, tudíž si ji představíme detailněji, včetně popisu klíčových míst realizace jednotlivých aktivit a úkolů. Oproti úloze 1 a 2 jde o aktivitu s větší časovou náročností.

Žáci obdrží pracovní list (viz http://www.hyperspace.cz/data/files/20/80/79broncos_pl.pdf) a samostatně pracují na prvních úkolech, které mají motivační charakter. Součástí úvodní části je krátké úvodní video (v anglickém jazyce), které představuje stadion amerického fotbalu Mile High Empower Field v Denveru, domovský stadion týmu Denver Broncos. Již ve videu je zmíněna problematika vlivu vysoké nadmořské výšky v souvislosti se sportovními výkony.

Text zadání se věnuje bilanci domácích a venkovních zápasů vybraných týmů v Denveru. Úkolem žáků je zamyslet se nad otázkou „Proč by se hostující týmy mohly více trápit, pokud hrají na stadionech v Denveru?“ a svůj odhad i zapsat do pracovního listu. Zároveň mají vyhledat zajímavé informace o Denveru, zejména ve vztahu k jeho poloze, a vysvětlit význam číslic 5280‘ v úvodním videu.

Hlavní část úlohy tvoří konkrétní případ, kdy v Denveru hraje tým Oakland Raiders, který má velmi dobrou sezónu, ale v zápase na stadionu v Denveru se mu herně nedaří. Hráči Oaklandu nejsou schopni své běžné hry, protože mají v novém prostředí zvýšenou tepovou i dechovou frekvenci, pociťují celkovou únavu a nedostatek energie. Denver, ačkoliv byl papírově slabší, nakonec tento zápas vyhrává s velkým náskokem.

Určitou nápovědou pro vyřešení problému je rovnice buněčného dýchání, v níž jsme záměrně ponechali chemické vzorce jednotlivých chemických látek. Žáci mají za úkol chemické látky pojmenovat a doplnit správné názvy do rovnice níže (pozn. v případě, že by ještě názvosloví neovládali, tak mohou vyhledat údaje například na internetu, jelikož jednotlivé názvy sloučenin lze bez problémů nalézt při zadání vzorce do internetového vyhledávače). Část 1 pracovního listu obsahuje již tři hlavní otázky: 1. Ve dvou až třech větách popište, jak hráč Oaklandu získává a využívá energii, aby mohl odehrát zápas.; 2. Za předpokladu, že hráči Raiders jedí před zápasem stejné jídlo jako obvykle, vysvětlete, co je pro hráče Raiders odlišné v porovnání se zápasy hranými na jejich domovském stadionu Oakland Coliseum či jiných stadionech, které se nacházejí na hladině moře.; 3. Vytvořte vlastní domněnku, proč Raiders pociťují větší únavu v Denveru. Své tvrzení podložte údaji o zvýšené srdeční frekvenci a dechové frekvenci.

Poté mají řešitelé prostor na to, aby uvažovali nad látkami a energií v rovnici buněčného dýchání a mají za úkol nakreslit model (například obrázek, diagram, schéma apod.), pomocí kterého by byli schopni vysvětlit, jakým způsobem hráč týmu Oakland Raiders získává a využívá energii, aby mohl odehrát zápas proti domácímu týmu na stadionu v Denveru. Lze říci, že řešení předchozích tří úkolů by jim mělo pomoci v tom, aby si každý žák sestavil vlastní model využívání energie hráče. Úkolem je zakreslit (zapsat) faktory, které jsou viditelné, ale i faktory, které na první pohled vidět nelze. Model má obsahovat i šipky a popisky, s jejichž pomocí je znázorněn tok energie a koloběh chemických látek.

Žáci představí své návrhy a následně o nich celá třída hromadně diskutuje. Po třídní diskuzi je vhodné žákům položit následující otázky: Co to znamená, že je vzduch řídký? Proč záleží na tom, zda je vzduch řídký? Jak by tato skutečnost mohla ovlivnit sportovní výkon domácích a hostujících týmů? Na základě odpovědí žáků provedeme stručné shrnutí hlavních myšlenek.

Další část (viz Část 2 v pracovním listu) tvoří možnost upravit vytvořený model tak, aby obsahoval všechny předepsané faktory či vlivy (hráč, kyslík, oxid uhličitý, voda, glukóza, energie), pokud je předchozí model neobsahoval. Pokyny k vypracování jsou shodné se zadáním u prvního modelu a žáci opět pracují ve dvojici. Mají takto možnost upravit svůj model dle nápadů, které slyšeli v rámci předchozí diskuze ve třídě k první části úlohy 3, popřípadě dle nových informací, které si mezitím dohledali. V této druhé části je zařazena i práce s tabulkou převzatou z odborného časopisu, v níž je popisována spotřeba kyslíku, tepová frekvence a minutový srdeční objem v závislosti na velikosti zátěže a nadmořské výšce. Žáci provedou výpočet minutového srdečního objemu, jehož hodnotu dají do souvislosti s hodnotami uvedenými v tabulce a s předchozími zjištěními při vytváření vlastního modelu. Je vhodné s žáky projít jednotlivé údaje v tabulce, jelikož se v ní vyskytuje několik veličin, včetně rozdílných jednotek. Z tohoto důvodu je v zadání úlohy 3 zařazena také otázka, ve které se mají žáci zamyslet nad tím, proč je v rovnici pro výpočet minutového srdečního objemu hodnota podílu násobena stem. Někteří žáci si takto mohou vlastnosti převodů jednotek i samostatně uvědomit.

Závěrečným úkolem žáků v úloze 3 je nalézt další podobná místa ve světě, kde by se sportovci mohli potýkat se stejnými problémy jako na stadionu v Denveru. Žáci mají uvést i názvy států, ve kterých se daná místa nachází a stručně své odpovědi vysvětlit.

Diskuze

Významným přínosem pro modernizaci a zkvalitnění kurikula, pro inovaci obsahu vzdělávání je Bloomův model taxonomie vzdělávacích cílů (Bloom el al., 1956). Jde o model přinášející přehled kognitivních, afektivních a psychomotorických cílů, který je nástrojem pro přechod od abstraktních cílů plánování výuky k jejich praktickému použití.

Jak jsme již uvedli, jedním z pedagogických aspektů integrace jiných disciplín do výuky matematiky je transformace poznatků určitého vědního oboru do obsahu kurikula (učiva) dalších disciplín, tedy výběr a stanovení základního integrovaného učiva. V tomto kontextu je příprava plánovaného kurikula (příprava na vyučovací hodinu) velice důležitým aspektem, dokonce stěžejním. Integrovaný způsob výuky totiž neumožňuje pouhé spoléhání se na učebnici (neexistují), ale naopak evokuje potřebu učební texty vytvářet a používat složitější technické prostředky, využít nové metody apod. Při plánování výuky je důležité stanovit si vzdělávací cíle podle jejich kognitivní náročnosti, v souladu například s Bloomovou taxonomií edukačních cílů.

Od roku 2001 pracujeme s revidovanou Bloomovou taxonomií (Anderson et al., 2001), s jejíž pomocí lze snadněji nalézt odpovědi na otázky: Co učit? Jak dosáhnout cíle? Jak hodnotit? Existuje koherence mezi cíli, instrukcemi a hodnocením? V následujícím textu se pokusíme diskutovat cíle úloh 1, 2 a 3 tak, jak bychom je hodnotili vzhledem k revidované verzi Bloomovy taxonomie (verze přeložená Hudecovou, 2004, s. 277; viz Tab. 1). Je na čtenáři, zda bude s naším hodnocením souhlasit, popřípadě si může provést své vlastní hodnocení, a tím si uvědomit související otázky s problematikou integrace vzdělávacích obsahů.

Tabulka 1: Hodnocení cílů úloh 1, 2 a 3 ve vztahu k revidované verzi Bloomovy taxonomie

Vysvětlivky: ① – úloha 1, ② – úloha 2, ③ – úloha 3

Úloha 1 je úlohou, která mezipředmětově využívá matematický aparát k vyřešení otázek z přírodopisu a z fyziky. Otázky v úloze jsou směřovány tak, aby došlo k propojení učiva všech vzdělávacích oblastí. Předpokládá proto aktivní znalosti ze tří vědních oborů. Mezipředmětový přesah je zde využit maximálně s viditelnou snahou o integraci. V úloze je patrné směřování k I) dimenzi zapamatování, porozumění a k aplikaci faktuálních znalostí, ale evidujeme také II) snahu žáky naučit důležitým konceptům a zdůraznění rozboru učiva na jeho základní části, odhalení vztahů mezi jeho částmi a pochopení způsobů, jak jsou tyto části uspořádané. Jednotlivé pojmy jsou v úloze propojeny, aby tvořily celek. Pojmy se v zadání úlohy kombinují tak, aby vytvořily strukturu, která předtím nebyla zřejmá.

Úloha 2 je označena jako aplikační úloha, která na základě vlastní aktivity žáků a statistického měření směřuje především k naplnění cílů vzdělávací oblasti Matematika a její aplikace. Mezipředmětový přesah je v této úloze využit spíše v aplikační rovině obsahu a je zde patrné směřování k dimenzi zapamatování, porozumění a k aplikaci faktuálních znalostí. Stejně jako úloha 1 směřuje k výše vymezeným dimenzím označeným jako I a II. Autoři dokonce chtějí, aby o pojmech v zadání žáci přemýšleli obecně.

Úloha 3 je aktivitou komplexní, která cílí velmi vysoko v edukačních cílech (viz tabulka 1). Je záměrně připravena jako úloha vhodná pro integrovanou výuku. Je nadstandardně rozsáhlá a lze říci, že se nejedná o dílčí úlohu, ale o komplexní aktivitu. Jejím cílem je integrace všech uvedených vzdělávacích oblastí tak, aby po vyřešení aktivity došlo k propojení znalostí mezi předměty a jeden pojem vyrůstal z druhého, z třetího atd. V úloze je samozřejmostí směřování k výše definovaným dimenzím I a II. Jednotlivé pojmy jsou v úloze propojeny tak, aby tvořily celek, pojmy se v zadání úlohy kombinují a vytvářejí strukturu, která předtím nemusela být zcela zřejmá. I v tomto případě autoři chtějí, aby žáci o pojmech v zadání přemýšleli v obecné rovině. Úlohu 3 hodnotíme jako aktivitu, která cílí na metakognitivní znalost, kterou autoři revidované Bloomovy taxonomie (viz Anderson et al., 2001) charakterizují jako znalost žáků, která se týká jejich vlastního poznávání (kognice) a kontroly nad svým vlastním poznáváním.

Závěr

V našem příspěvku jsme si představili tři konkrétní úlohy, které mají ambice pro využití při integrované nebo mezipředmětové výuce. Při porovnání s revidovanou verzí Bloomovy taxonomie se ukazuje, že každá úloha cílí na různé vzdělávací cíle. Netvrdíme však, že úloha 3 je jediná správná. Je velmi žádoucí, aby se žáci setkávali s úlohami různé obtížnosti a reflektujícími různé úrovně vzdělávacích cílů. Cílem našeho příspěvku je uvědomit si problematiku vytváření a využívání integrovaných či mezipředmětových úloh. Na vybraných příkladech jsme ukázali, že je možné integrovat dvě, tři i více vzdělávacích oblastí nebo je spojit v mezipředmětovém kontextu pro dosažení předem stanoveného cíle. Volba integrovaného přístupu k výuce závisí na zdatnosti učitele, který musí být obeznámen se školním kurikulem jednotlivých předmětů, spadajících pod integrované vzdělávací oblasti. Potenciál má také využívání tandemové výuky, na které se podílejí učitelé daných předmětů. Z uvedených vyjádření, přístupů a konceptů v našem příspěvku vyplývá, že přístup učitele k výuce ovlivňuje charakter poznatků, které si žáci z výuky odnesou. Přístupů je obecně mnoho a jejich volba záleží na učiteli samotném, na jeho znalostech, dovednostech, zkušenostech a také na jeho odvaze začínat něco nového.

Doc. RNDr. Helena Koldová, Ph.D.

Je absolventkou učitelství oborů matematika a fyzika na pedagogické fakultě v Českých Budějovicích. Působila jako učitelka na střední škole strojírenské v Českých Budějovicích. Od roku 1999 působí na Pedagogické fakultě Jihočeské univerzity v Českých Budějovicích. Věnuje se didaktice matematiky, připravuje studenty oboru učitelství 1. stupně i učitele matematiky 2. stupně. Je spoluautorkou řady učebnic matematiky pro 2. stupeň základní školy, řady učebnic pro školy střední a autorkou mnoha odborných publikací v oblasti didaktiky matematiky u nás i v zahraničí. V současné době se věnuje problematice integrované výuky (CLIL, STEM).

Kontakt: hbinter@pf.jcu.cz

Mgr. Lukáš Rokos, Ph.D.

Vystudoval učitelství biologie a chemie pro střední školu, následně se v rámci doktorského studia věnoval problematice badatelsky orientované výuky v přírodopisu a biologii. Působí jako odborný asistent na katedře biologie Pedagogické fakulty Jihočeské univerzity v Českých Budějovicích. V současné době se věnuje problematice integrované STEM výuky, možnostem využití formativního hodnocení a otázkám pregraduální přípravy studentů učitelství přírodovědných předmětů.

Kontakt: Lrokos@pf.jcu.cz

Literatura

Anderson, L. W., Krathwohl, D. R., Airasian, P. W., Cruikshank, K. A., Mayer, R. E., Pintrich, P. P., Raths, J., & Wittrock, M. (2001). A Taxonomy for Learning, Teaching a Assesing of Educational Objektives. Longman.

Berlandová, L. K., & Steingutová, R. (2016). Explaining variation in student efforts towards using math and science knowledge in engineering contexts. International Journal of Science Education, 38(18), 2742–2761.

Binterová, H., Fuchs, E., & Tlustý, P. (2008). Matematika 7 – Geometrie. Fraus.

Bloom, B. S., Englenhart, D., Fursdt, E. J., Hill, W. H., & Krathwohl, D. R. (1956). The Taxonomy of Educational Objectives. The Clasifications of Educational Goals, Handbook I: Cognitive Domain. David Mc Key Company.

Brlicová, V., Cizlerová, M., Mahel, M., Svobodová, J., Vach, P., Žák, L., & Žáková, L. (2022). Matematika pro život 8 – Učebnice. Didaktis.

Dareová, E., Ellis, J., & Roehrigová, G. (2018). Understanding science teachers’ implementations of integrated STEM curricular units through a phenomenological multiple case study. International Journal of STEM Education, 5(4), 1–19.

Hudecová, D. (2004). Revize Bloomovy taxonomie edukačních cílů, Pedagogika, 54(3), 274–283.

Janás, J. (1985). Mezipředmětové vztahy a jejich uplatňování ve fyzice a chemii na základní škole. Ústí nad Labem: Univerzita J. E. Purkyně.

Koldová, H., Petrášková, V., Novotná, J., Moraová, H., Samková, L., Jordánová, D., Kazda, M., & Reslová, H. (2020). Integrovaná výuka z pohledu výuky matematiky. Jihočeská univerzita v Českých Budějovicích, Pedagogická fakulta.

Kovaliková, S., & Olsenová, K. D. (1995). Integrovaná tematická výuka: model. Spirála.

MŠMT (2021). Rámcový vzdělávací program pro základní vzdělávání. Praha.

NPI (2022). Tisková zpráva – Škola budoucnosti je o další krok blíž. To hlavní z Hlavních směrů revize RVP ZV po vypořádání připomínek (on-line, cit. 2022-06-23). Dostupné z: https://www.npi.cz/images/tiskove_zpravy/hlavni_smery_revize_rvp_zv.pdf

Podroužek, L. (2002). Integrovaná výuka na základní škole v teorii a praxi. Plzeň: Fraus.

Průcha, J., Walterová, E., & Mareš, J. (2003). Pedagogický slovník. Praha: Portál.

Rakoušová, A. (2008). Integrace obsahu vyučování. Praha: Grada.

Skalková, J. (2006). K některým aktuálním problémům všeobecného vzdělání v kontextu učící se a globalizující se společnosti. Pedagogická orientace, 1, 2–17.

Odkazy v textu

^[1] Rámcový vzdělávací program pro základní vzdělávání aktuálně prochází revizí a nové pojetí by mělo být připraveno do podzimu 2023. Jedním z cílů je propojení očekávaných výstupů s klíčovými kompetencemi. Základní gramotnosti (čtenářská a matematická) by se měly prolínat všemi oblastmi a obory (NPI, 2022).

V době psaní tohoto příspěvku byla k dispozici pouze tisková zpráva a stručný přehled vizí, tudíž se může stát, že některé nové přístupy zde nejsou reflektovány.